実験計画法2
こんにちは先端技研の中根です。本日は実験計画法に関してその基本となる1元配置実験について説明しようと思います。統計用語が多く出てきますがわかりやすく説明しようと思います。
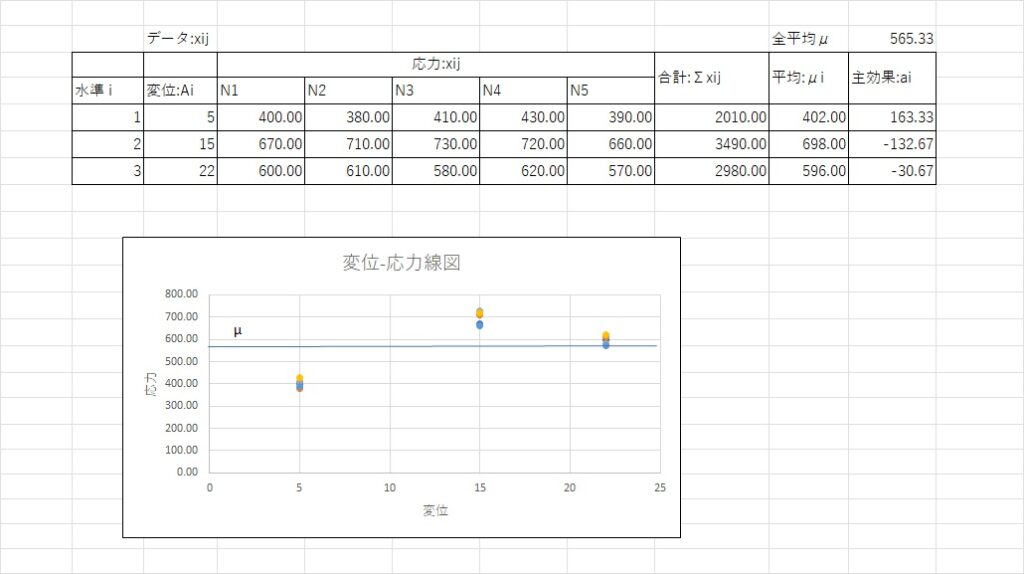
1元配置の実験は基本的なデータの取り方で、一つの因子を変化させて影響を調べる実験です。一因子実験と言えばわかると思います。上表は引っ張り試験機で試験片を5、15、12変位(Ai)させた時の応力:Xijです(変位-応力線図)。試験片は5本用意して、それぞれ実験をした結果です。応力Xijにはバラツキがあることがわかります。このばらつきは実験結果を観察する上で許容できるバラツキであるのか分散分析によって判断しようとします。
①まずは全ての応力Xijの全平均μを計算します。
②次に各変位に対する平均μiを計算します。
③次に(全平均μ – 各平均μi)を各変位に関して計算します。(主効果ai)
主効果という言葉は聞きなれないかもしれませんが因子(応力)が水準(変位)を変えることで生じる効果のことです。
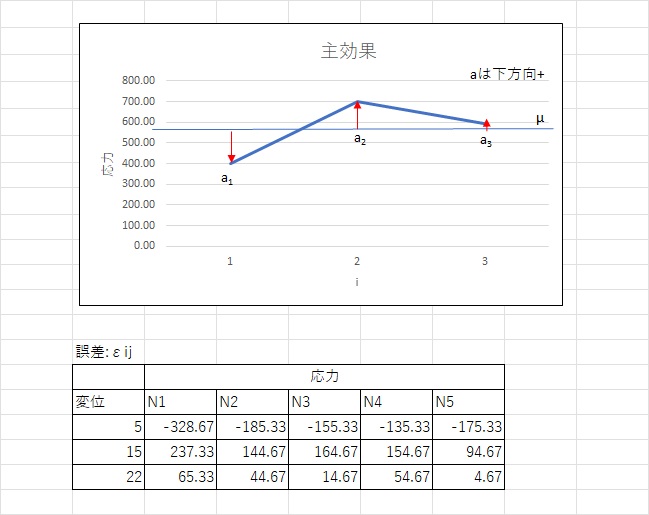
応力の主効果をグラフにすると上図のようになります。横軸に水準i(1、2,3)をとり縦軸に各応力の平均μiの応力をとります。主効果ai =(全平均 μ- 各平均μi)なので下矢印の方向が正になります。
各応力の誤差εijも計算しておきましょう。計算はεij = xij – μ – aiで計算します。式を少し変形すると
xij = μ + ai +εij = (全体平均)+(主効果)+(誤差)
これを実験計画法では重要な概念で、データの構造式と呼びます。ちなみに主効果aiの総和は0になります。
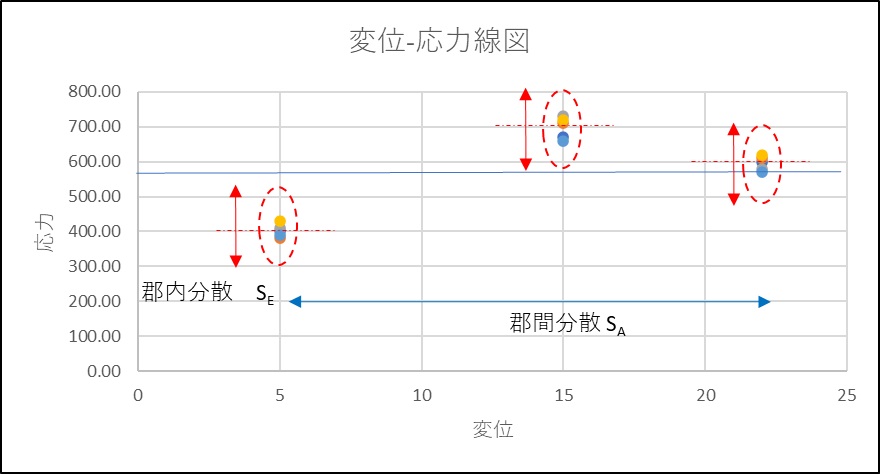
いよいよ、分散分析に入ります。分散分析で何を計算しているのか説明します。
分散は同じ変位でのデータ間に生じる分散である郡内分散と異なる変位間で生じる分散である群間分散が生じます。分散を求めるにはまずデータの2乗和を計算する必要があります。まず全データの2乗和STを計算、群間2乗和 SAを計算、最後に群内2乗和 SEを計算しますが ST = SA + SE の関係が成り立つので群内2乗和SE = ST – SA で計算できます。但し分散精度を上げるために修正項というデータ合計の2乗をデータ数で割った数値を引いています。
次に自由度を計算します。何故自由度を計算するかはこの後に計算する分散計算のためと統計学のF検定で使用するためです。自由度とはデータのとりうる数です。例えばxijのデータ数は15個ですが14個まで決まれば最後のデータは自ずと決まってしまうので15-1=14になります。
最後にSA、SEを自由度で割って、群間分散VAと郡内分散VEを求め、F検定を行うためのF0値をF0 = VA / VEで計算します。このF0値と自由度からP値を求めますがExcel関数のF.DIST.RT関数で導くことができます。このP値が5%(0.05)以下ならば有意、1%(0.01)以下ならば非常に有意であると判断します。
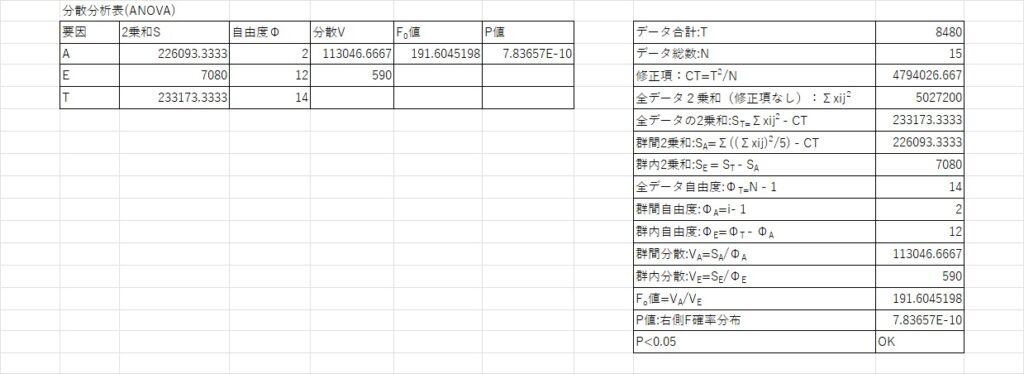
それでは実際に分散分析の計算をしてみましょう。分散分析を行うためには上表のような分散分析表を作る必要があります。右の表は分散分析表を作るための計算補助表になります。
まずはこの計算補助表を作成しましょう。数式がかかれているのでわかると思いますが群間2乗和SAは各水準iの合計の2乗をN数である5で割った後、総和をとって修正項CTを引いています。
F0値はデータの誤差に対する比率なので大きい方がデータの信頼度が上がってきます。計算補助表の結果を分散分析表に割り当てると上表のようになります。
最後に右側F分布によって検定を実施します。P値<0.01(1%)であるので、このデータは非常に有意であると判断でき群間差あり、つまり郡内分散に対して群間分散がしっかりと出ており、信頼できるデータと判断できます。
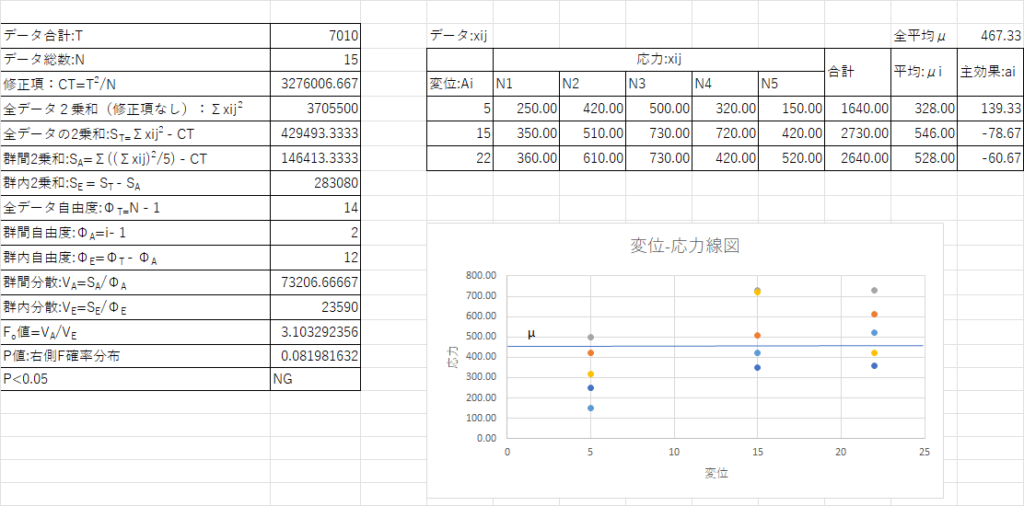
参考までに上のデータはP値 > 0.05(5%)なので誤差要因が大きく、有意ではないと判断されます。ちなみにExcelのデータ分析で分散分析:1元配置実験で分散分析表は一瞬で計算できます。しかし、どのような計算をしているのか理解することも必要と考え説明いたしました。
いかがでしたでしょうか、実験計画法のはじめの一歩ですが理解いただけたでしょうか?次回は2元配置実験の説明をいたします。
最後までお読みいただきありがとうございます。