実験計画法3
こんにちは先端技研の中根です。前回の1元配置実験に続いて今回は2元配置実験について説明します。それでは前回の復習からはじめます。1元配置実験というのはパラメータ(因子)がひとつで、複数の水準でのデータでした。そしてデータのパラツキが有意であるかを分散分析で検定しました。2元配置の実験でもやることは同じです。しかし、2元配置実験では実験の効果として交互作用を確認することができます。それでは実際のデータを見てみましょう。
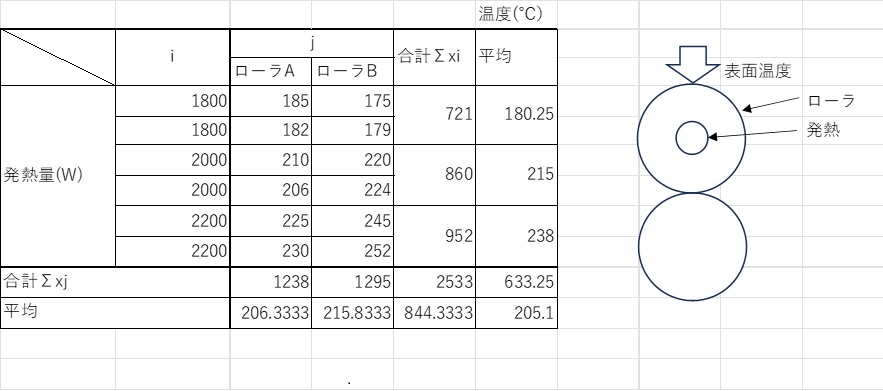
このデータはローラ内部にヒータを配置して、一定時間経過した後のローラ表面温度を計測した結果です。発熱量1800W、2000W、2200Wで、それぞれ2回測定した結果です。但しデータはフィッシャーの3原則による反復、無作為化により計測しています。つまり2回の測定でその順番はサイコロで決めて時間をずらして測定するようにします。これを実験計画法では「繰り返しのある実験」と言います。これにより誤差を偶然誤差として、取り扱うことができます。このままだと傾向がよくわからないのでグラフ化してみます。
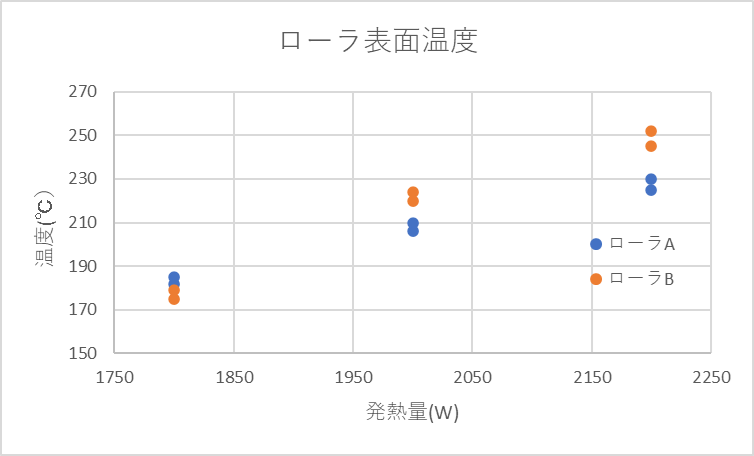
グラフを見るとローラA、Bで温度上昇率が異なることがわかると思います。このような場合、ローラA、ローラBの因子間に交互作用があるといいます。交互作用がない場合はローラA、B間が平行になった場合になります。それではローラA、Bの主効果および交互作用が誤差に対して有意であるか分散分析を使って確かめていきましょう。
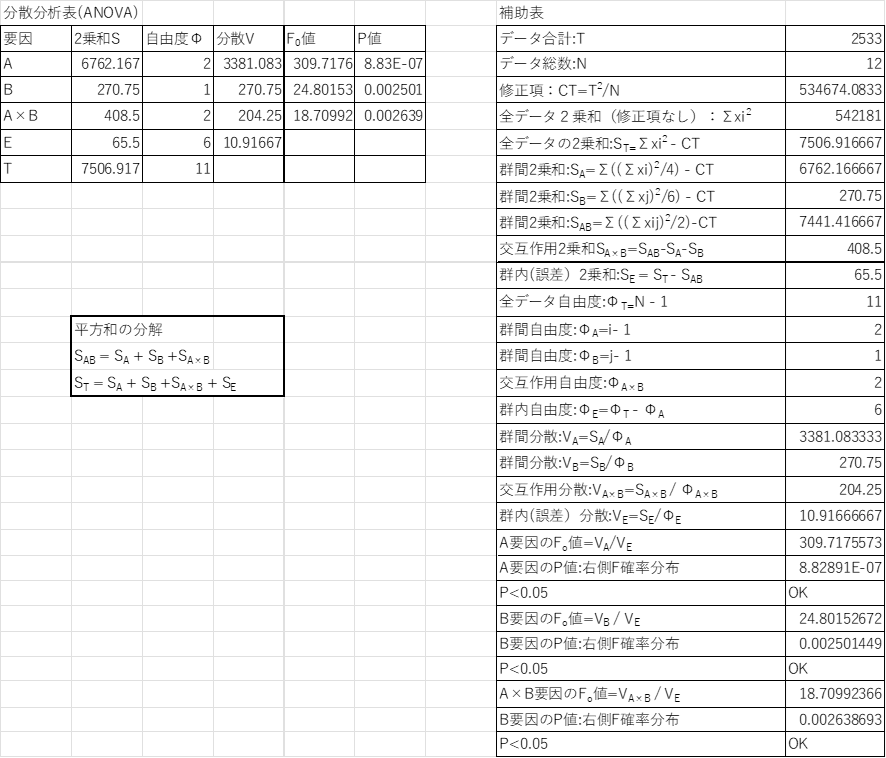
1元配置実験に比べて複雑になってきましたが計算の考え方は同じです。まず右側の補助表の計算をします。最初に2乗和を計算します。2元配置なので要因A、Bに加えて要因ABが加わってきます。要因ABの2乗和計算は各繰り返しデータを加算後、2乗後2で割り加算後、修正項CTで引きます。
SAB={(185+182)2/2+(210+206)2/2+・・・・+(245+252)2/2}- CT
となります。誤差2乗和も平方和の分解公式からSE = ST – SABで計算ができます。
次に要因A×BつまりAとBの交互作用の2乗和SA×Bを計算しますがこれは平方和の分解という便利な公式があるので、これを変形してSA×B = SAB – SA – SB で計算をします。
2乗和の後は自由度の算出ですが自由度の考え方は前回説明したので、省略します。まず要因Aは発熱量でありi=3なのでΦA = 3 – 1 = 2となります。要因Bはj=2なので
ΦB = j – 1 = 1、交互作用A×Bの自由度はΦA×B = ΦA × ΦB = 2×1=2となります。
最後に各分散の計算を計算して、誤差分散VEとの比をとりF0値を計算してF確率分布による検定を要因A、B、交互作用A×Bそれそれで計算します。計算方法は1元配置実験と同じなので説明を省略します。補助表が完成したらその結果を左側の分散分析表に入れます。各要因のP値を確認すると要因A、B、交互作用A×Bどれも5%以下になっていることがわかります。この結果から要因A、B、交互作用A×Bの要因が信頼できるものと判断できます。つまり上のローラ表面温度に示す主効果、交互作用が確かに確認できることが検証できたことになります。
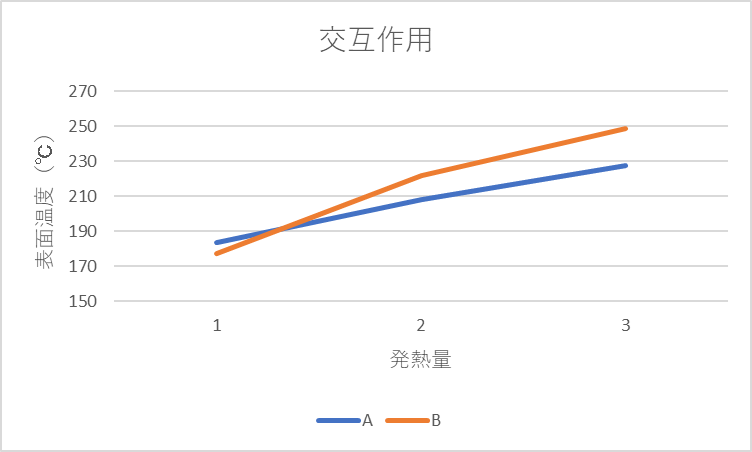
最後に3種類の発熱量とローラ表面温度の折れ線グラフを表記します。これを見るとローラA、Bで交互作用があることがわかります。ちなみに一元配置実験と同様に繰り返しのある2元配置実験もExcelのデータ分析にありますので、興味がありましたらご自分でとったデータの分散分析を実施してみるとよいと思います。
いかがでしたでしょうか?実験データが誤差に対して有意であることを証明するにはこのような手順が必要になります。ここまで理解した上で、次はいよいよ実験計画法の本丸である直交配列表実験の説明をしていきます。
最後までお読みいただきありがとうございました。