実験計画法4
直交表を使った実験計画
こんにちは先端技研の中根です。本日は直交表を使った実験計画について話をします。ここまで1元配置実験と2元配置実験の説明をしてきましたが因子の数が3個、4個、5個と増やした時の主効果や交互作用を確認するのはどうしたらよいでしょうか?例えば因子の水準が2個だった場合、総あたり実験をするには因子数3個の場合23=8通り、4個の場合24=16通り、5個の場合25=32通りと指数的に増加していきます。時間があれば総あたりの実験をしてもよいのですが、ほとんどの方が時間を節約したいと考えているはずです。そんな時に実験回数を減らすことができる便利な直交表があります。(直行表ではないので注意)それでは実験計画を立ててみます。
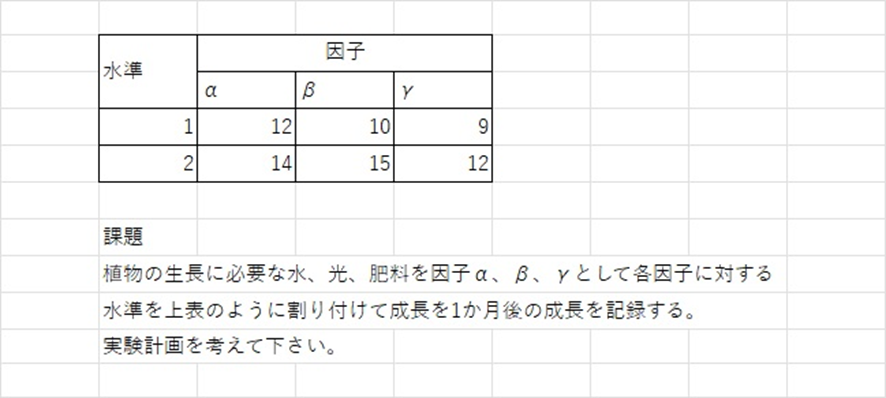
上のような課題を用意してみました。3つの因子α、β、γにそれぞれ2つの水準値が割り付けられています。この実験計画を考えてみて下さい。総あたり実験をすると2×2×2=8通りの実験になります。8通りぐらいなら苦にならないと思われるかもしれませんが因子がさらに増えると総あたり実験は現実的ではないと思います。
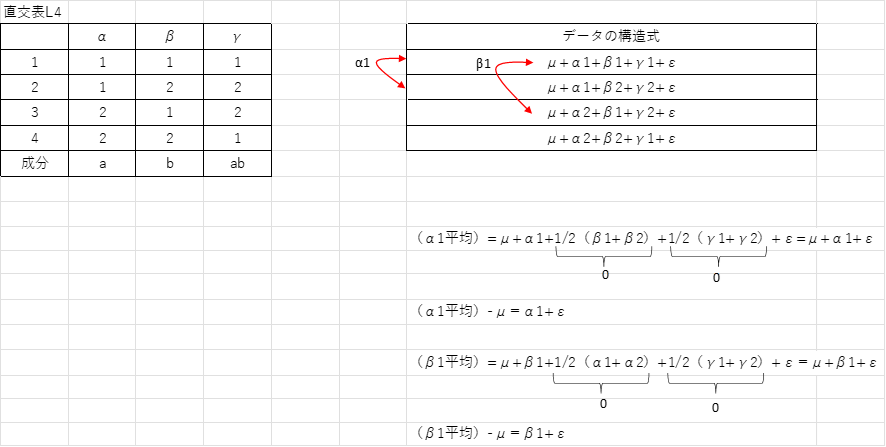
上左図は直交表L4になります。直交表というのは実験を間引く事ができる便利なツールと考えて下さい。この表の見方は列に因子が、行に実験が割り付けられています。注目してほしいのは因子列α、β、γで任意の2列を選んだ時に因子水準1、2がそれぞれ均等に表れていることです。そして一番下には成分と書かれた行があります。これは後述しますが交互作用の成分を示したものです。つまり、総あたり実験で8回実施しなければならないものが4回の実験で済むことになります。例えば1行目の実験1ではα1、β1、γ1の組み合わせで実験を行います。
それでは何故8回の実験が4回の実験で済むのか簡単に説明します。実験計画法では要因α、β、γの主効果を見るために右にあるようなデータの構造式で表します。μは全平均、α1、β1、γ1は要因α、β、γの水準1における主効果、α2、β2、γ2は要因α、β、γにおける水準2における主効果、εは誤差です。このデータ構造式から主効果を計算します。主効果は各要因の平均から全平均を引いた値なので、まずα1を含む直交表L4の1、2行の実験のデータ構造式からα1平均を計算します。

ところがα1およびα2は上図に示すように全平均μからの距離になるのでα1+α2=0になります。同様にβ1+β2=0、γ1+γ2=0になるので上式(α1平均)はβ1+β2の項、γ1+γ2の項が0になるので(α1平均)=μ+α1+εになります。よって(α1平均)-μ=α1+εに変形できるのでα1の主効果を求めることができます。同様に直交表L4の1行目と3行目からβ1の主効果を求めることができ、α2、β2、γ1、γ2の主効果も求めることができます。もちろん総あたり実験をしても構造式から各主効果を求めることができますが実験を間引くことができるので直交表を用いた方が効率的です。
直交表は2水準系でL8、L16、L32、3水準系でL9、L27、混合系でL18、L36と色々ありますので、実験したい因子の数や水準に応じて使い分ける必要があります。後は前回説明した分散分析を実施して各要因の有意を確認した後、主効果と交互作用を検証する流れになります。
最後に実験計画法における交互作用ですが直交表L4の最終行に成分と書かれています。これは因子α、βの成分a、bの交互作用成分abがγ列に現れることを意味しています。つまり要因γはγの主効果の他にα、βの交互作用成分が入ってくることを意味します。ここが実験計画法が難しいといわれる部分で、各主効果を正確に見たいのであれば交互作用のでない因子α、βを実験に割り付ける必要があります。また要因α、βの主効果のみをみたいのであれば要因γを直交表に割り付けないという方法もあります。直交表L4ならば規模が小さいのでわかりやすいですが規模の大きい直交表を使うと交互作用列も多くなるので実験の割り付けには経験が必要になります。
このように実験計画法はうまく使えば効率アップおよび実験の確からしさを検証できます。実際、多くの企業で実験計画法を使い、成果を上げています。
いかがでしたでしょうか?本日は直交表を使った実験計画について説明しました。次回はシミュレーションにおける実験計画法の説明をいたします。 最後までお読みいただきありがとうございます。