品質工学MTシステムに関して2
こんにちは先端技研の中根です。前回はマハラノビスの距離について説明しました。データの判別に使用できることが理解できましたでしょうか?それではMTのT(タグチ)は必要ないのではないかと思われた方いませんでしょうか?田口先生はマハラノビスの距離を使って原因診断まで考えたのです。データの特徴量を多数とり、その中から何が原因で判別されたのか知りたいとは思いませんか?
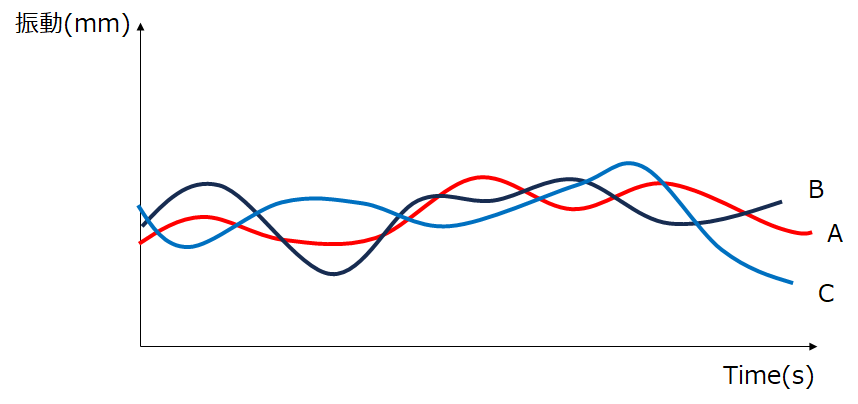
具体的な例で説明します。上図はある製品の振動レベルの経時変化です。この振動が異常振動か調べるためには製品の正常状態の振動データを集める必要があります。ちょっと見ただけではどこが異常振動なのかわかりませんよね。異常かどうかを判断するにはたくさんの正常な振動レベルのデータが必要です。異常なデータをたくさん集めてもデータの異常性は判断できないのです。理由はデータの異常性はそれぞれ個々に違うからなのです。
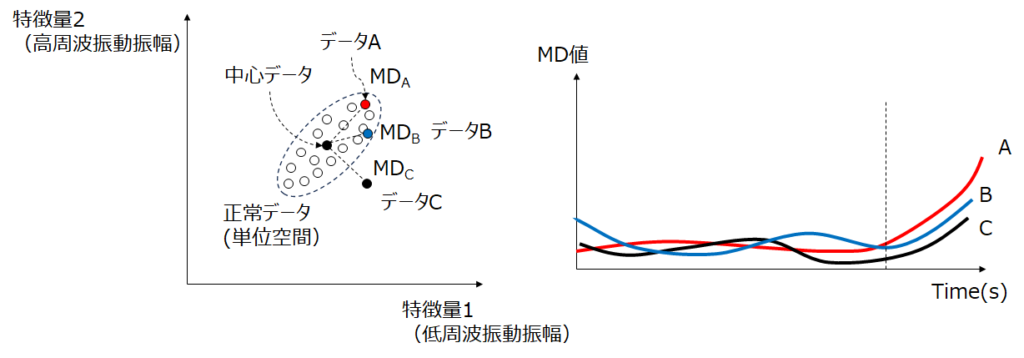
左の図は振動データの特徴量を特徴量1(低周波数振動振幅)と特徴量2(高周波振動振幅)とした時の散布図です。中央の楕円部分がデータA、B、Cの正常データ群です。これを単位空間と呼びます。そして単位空間の中心からデータA、B、Cまでのマハラノビスの距離MDA、MDB、MDC(前回のブログ参照)を計算します。
そして右のグラフがデータA、B、Cのマハラノビスの距離MD値の推移になります。このグラフを見ると破線部から各MD値が増加しているのがわかりますよね。
このように一見するとデータの異常性が確認できなくてもMD値(マハラノビスの距離)にするとわかりますよね。また予兆も見えてくると思います。
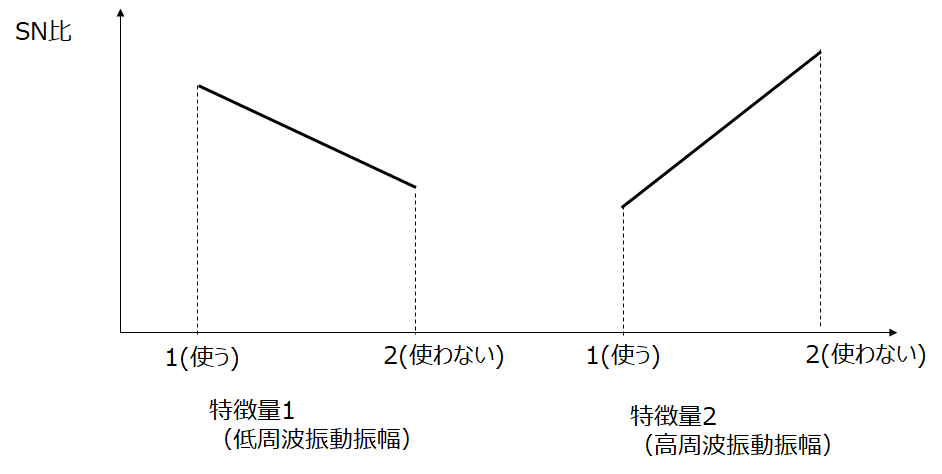
MD値を計算した後に重要になるのが項目診断になります。MTシステムではデータを2水準系直交表に割り付けてSN比を計算しています。1がデータを使う場合、2がデータを使わない場合になります。それぞれに対してデータ異常の判別に貢献しているか、していないかをSN比で判別しています。上のグラフは要因効果図というグラフでこのグラフをもとに異常データとなった原因を突き止めます。SN比が高い方がデータ判別に貢献していると考えて下さい。
これをみると特徴量1、つまり低周波振動振幅の方がSN比が高く判別に貢献していますね。逆に特徴量2の高周波振動振幅の方は貢献していないのがわかります。つまり特徴量1の低周波振動が原因で振動の異常性が判別できたことになります。
どうでしょうか?何が原因で異常振動と判別したのかわかるとデータに納得できると思います。私は古い人間なのでデータに振り回されるよりは納得しなが進めていく方が合っていますのでこのMTシステムは良いと思います。今日はMTシステムについて説明しました。次回はその他のMTシステムについて説明します。
最後までお読みいただきありがとうございます。